The History | Definition | Breakdown of the Equation

The History

The parabola was explored by Menaechmus (380 BC to 320 BC), who was a pupil of Plato and Eudoxus. He was trying to dublicate the cube by finding the side of the cube that has an area double the cube. Instead, Menaechmus solved it by finding the intersection of the two parabolas x2=y and y2=2x. Euclid (325 BC to 265 BC) wrote about the parabola. Apollonius (262 BC to 190 BC) named the parabola. Pappus (290 to 350) considered the focus and directrix of the parabola. Pascal (1623 to 1662) considered the parabola as a projection of a circle. Galileo (1564 to 1642) showed that projectiles falling under uniform gravity follow parabolic paths. Gregory (1638 to 1675) and Newton (1643 tp 1727) considered the properties of a parabola.

all my best features were exagerrated... how's my chin? i look sad because i was locked in my room for being a threat to my parental units aka. society i pluck my own eyebrows
ApolloniusGalileoPascalEuclid

Definition

A parabola is a set of all points that are the same distance from a fixed line (directrix) and a fixed point (focus) not on the directrix.

The parabola is also classified as a member of the family of conic sections, which includes the circle, ellipse, and hyperbola. A conic section is defined as intersections of a plane and a cone. A parabola is defined as a plane that intersects a cone when it is slanted at the same side of the cone (or parallel to the slant height).

Watch a movie to see the parabola as a projection of a circle and as the set of all points equidistant from the focus and the directrix.




Breakdown of the Equation


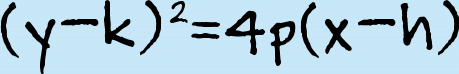
Standard Form when the directrix is parallel to the y-axis.


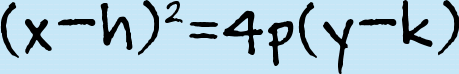
Standard Form when the directrix is parallel to the x-axis.

1. (h, k) : Vertex of the Parabola
The vertex is where the parabola intersects its axis (aka axis of symmetry). The vertex is also the midpoint of the segment of the axis between the focus and the directrix.

See the Effects of h!

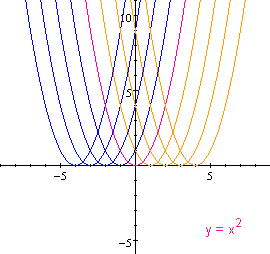When h is a negative integer, the graph moves to the left of the origin (0,0). When h is a positive integer, the graph moves to the right of the origin.

See the Effects of k!

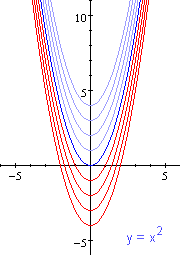When k is a negative integer, the graph moves towards the bottom of the graph, below the origin (0,0). When k is a positive integer, the graph moves towards the top of the graph, above the origin.

2. |p| : Distance from the Vertex
Indicates how far the directrix and the focus are from the vertex, because they are both equidistant from the vertex.

3. p : Direction Parabola Opens
The parabola opens upwards when p is positive and downwards when p is negative.

When p > 1, the parabola is wider than when p < 1.

What happens when p is negative?!

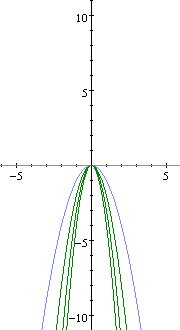When the variable p is negative, the graph opens downwards.

What happens when p is positive?

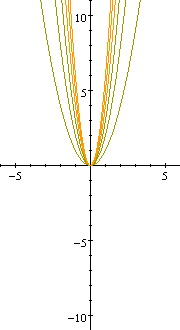When the variable p is positive, the graph opens upwards.

4. (h+p, k) when p is positive or (h, k+p) when p is negative : Focus

5. y : Directrix

6. x : Axis

7. 4p : Length of the Latus Rectum
The latus rectum is the chord through the focus and parallel to the directrix.

8. General Form : Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 is a parabola when A=0 or C=0

9. Eccentricity ALWAYS = 1

Other Variations of the equation:
(x-k)2=4p(y-h)
y=ax2+bx+c
y=a(x-p)2+q


go to

or go to previous page